Accueil

Préparation rentrée 2025

• Feuille de route de révisions
• DM n°Été
• Cahier d'entraînement
• Démonstrations exigibles du cours de PTSI
• Vocabulaire de la chimie
• Rappels de cristallographie
• Rappels d'induction et sur les forces de Laplace
• Polycopié CT
• Polycopié CM
• PTSI-TD-0
• PTSI-TD-1
• PTSI-TD-2

Travail personnel (mis à jour le 21 août 2025)

• Voir #Préparation de la rentrée.
• Terminer le DM d'Été, venir avec votre copie et préparer des questions.
• Réviser Induction et forces de Laplace, Cristallographie, Électrocinétique. Venir avec les affaires de PTSI correspondantes.
• Travailler les TD de révisions.

---

Tout au long de l'année, pour s'entraîner en autonomie :

• QCM de l'appli QMax
• Cahier d'entraînement Première année
• Cahier d'entraînement Deuxième année

Programmes de colle

Colle n°1 -- du 8 septembre au 12 septembre

Ondes et signaux (Rappels)

contenus

capacités exigibles

Filtrage linéaire Signaux périodiques. Fonction de transfert harmonique. Diagramme de Bode. Modèles de filtres passifs : passe-bas et passe-haut d’ordre 1, passe-bas et passe-bande d’ordre 2.

Analyser la décomposition fournie d’un signal périodique en une somme de fonctions sinusoïdales. Définir la valeur moyenne et la valeur efficace d’un signal. Établir par le calcul la valeur efficace d’un signal sinusoïdal. Interpréter le fait que le carré de la valeur efficace d’un signal périodique est égal à la somme des carrés des valeurs efficaces de ses harmoniques. Tracer le diagramme de Bode (amplitude et phase) associé à une fonction de transfert d’ordre 1. Utiliser une fonction de transfert donnée d’ordre 1 ou 2 (ou ses représentations graphiques) pour étudier la réponse d’un système linéaire à une excitation sinusoïdale, à une somme finie d’excitations sinusoïdales, à un signal périodique. Utiliser les échelles logarithmiques et interpréter les zones rectilignes des diagrammes de Bode en amplitude d’après l’expression de la fonction de transfert. Mettre en œuvre un dispositif expérimental illustrant l’utilité des fonctions de transfert pour un système linéaire à un ou plusieurs étages. Choisir un modèle de filtre en fonction d’un cahier des charges. Expliciter les conditions d’utilisation d’un filtre en tant que moyenneur, intégrateur, ou dérivateur. Expliquer l’intérêt, pour garantir leur fonctionnement lors de mises en cascade, de réaliser des filtres de tension de faible impédance de sortie et forte impédance d’entrée. Expliquer la nature du filtrage introduit par un dispositif mécanique (sismomètre, amortisseur, accéléromètre, etc.). Étudier le filtrage linéaire d’un signal non sinusoïdal à partir d’une analyse spectrale. Détecter le caractère non linéaire d’un système par l’apparition de nouvelles fréquences. Capacité numérique : simuler, à l’aide d’un langage de programmation, l'action d'un filtre sur un signal périodique dont le spectre est fourni. Mettre en évidence l'influence des caractéristiques du filtre sur l'opération de filtrage.

Questions de colles PTSI n°1

Questions (cliquer pour afficher/cacher) Représenter la maille c.f.c.. Déterminer la population et la compacité. Représenter la maille c.f.c.. Localiser les sites tétraédriques, les dénombrer en justifiant et déterminer leur habitabilité. Représenter la maille c.f.c.. Localiser les sites octaédriques, les dénombrer en justifiant et déterminer leur habitabilité. Établir les équations mécanique et électrique des rails de Laplace utilisés comme un moteur, c’est-à-dire fermés sur un générateur extérieur de fém $E_{0}$. On tiendra compte de la résistance $r$ des rails. Établir les équations mécanique et électrique des rails de Laplace utilisés comme un générateur, c’est-à-dire dont la tige mobile est tractée par une force constante ${\overrightarrow {F}}_{0}$. On tiendra compte de la résistance des rails. Procéder au bilan de puissances sur l’un des deux exemples précédents et l’interpréter. Les équations électrique et mécanique seront données par l’interrogateur. Définir le moment magnétique d’une spire plane et rappeler (sans démonstration) l’expression du couple de Laplace qu’elle subit lorsqu’elle est placée dans un champ magnétique uniforme. Un schéma est indispensable pour définir correctement les orientations. Rappeler le modèle du transformateur idéal et établir la loi des tensions.

Réponses (cliquer pour afficher/cacher) Pour la représentation, voir Rappels de cristallographie. Population : $Z=8/8+6/2+1=4$. Compacité : ${\mathcal {C}}=\pi {\sqrt {2}}/6$. Pour la représentation, voir Rappels de cristallographie. Ils sont aux centres des huit huitièmes de cube et donc au nombre de huit et leur habitabilité est $R+R_{T}={\frac {a{\sqrt {3}}}{4}}$. Pour la représentation, voir Rappels de cristallographie. Ils sont aux milieux des douze arêtes et au centre du cube et donc au nombre de quatre (12/4+1) et leur habitabilité est $R+R_{O}={\frac {a}{2}}$. Voir cours de PTSI. Voir cours de PTSI. Pour obtenir un bilan de puissances électriques, on multiplie l'équation électrique par l'intensité du courant. Pour obtenir un bilan de puissances mécaniques, on multiplie l'équation mécanique par la vitesse. Une spire parcourue par une intensité de courant i est orientée selon ce courant par la règle de la main droite, ce qui définit le vecteur normal unitaire ${\vec {n}}$. En notant S l'aire de la surface plane enlacée par le contour, son moment magnétique est défini par ${\vec {m}}=iS{\vec {n}}$. Quand elle est placée dans un champ magnétique uniforme ${\vec {B}}$, elle subit le couple de Laplace ${\vec {\mathcal {\Gamma }}}_{Lapl}={\vec {m}}\wedge {\vec {B}}$. Un transformateur idéal se modélise par deux bobinages autour d’un noyau ferromagnétique parfait dont on admet qu’il canalise parfaitement les lignes de champ magnétique. Par conséquent, le flux $\Phi$ au travers d’une spire du bobinage primaire est égal au flux au travers d’une spire du bobinage secondaire. Le résultat s’obtient en appliquant la loi de Faraday aux deux bobinages en tenant compte du nombre de spires : en régime variable (et au signe près sur les orientations), ${\frac {u_{2}}{N_{2}}}={\frac {u_{1}}{N_{1}}}$.

Colle n°2 -- du 15 septembre au 19 septembre

Ondes et signaux (Rappels)

contenus

capacités exigibles

Filtrage linéaire Signaux périodiques. Fonction de transfert harmonique. Diagramme de Bode. Modèles de filtres passifs : passe-bas et passe-haut d’ordre 1, passe-bas et passe-bande d’ordre 2.

Analyser la décomposition fournie d’un signal périodique en une somme de fonctions sinusoïdales. Définir la valeur moyenne et la valeur efficace d’un signal. Établir par le calcul la valeur efficace d’un signal sinusoïdal. Interpréter le fait que le carré de la valeur efficace d’un signal périodique est égal à la somme des carrés des valeurs efficaces de ses harmoniques. Tracer le diagramme de Bode (amplitude et phase) associé à une fonction de transfert d’ordre 1. Utiliser une fonction de transfert donnée d’ordre 1 ou 2 (ou ses représentations graphiques) pour étudier la réponse d’un système linéaire à une excitation sinusoïdale, à une somme finie d’excitations sinusoïdales, à un signal périodique. Utiliser les échelles logarithmiques et interpréter les zones rectilignes des diagrammes de Bode en amplitude d’après l’expression de la fonction de transfert. Mettre en œuvre un dispositif expérimental illustrant l’utilité des fonctions de transfert pour un système linéaire à un ou plusieurs étages. Choisir un modèle de filtre en fonction d’un cahier des charges. Expliciter les conditions d’utilisation d’un filtre en tant que moyenneur, intégrateur, ou dérivateur. Expliquer l’intérêt, pour garantir leur fonctionnement lors de mises en cascade, de réaliser des filtres de tension de faible impédance de sortie et forte impédance d’entrée. Expliquer la nature du filtrage introduit par un dispositif mécanique (sismomètre, amortisseur, accéléromètre, etc.). Étudier le filtrage linéaire d’un signal non sinusoïdal à partir d’une analyse spectrale. Détecter le caractère non linéaire d’un système par l’apparition de nouvelles fréquences. Capacité numérique : simuler, à l’aide d’un langage de programmation, l'action d'un filtre sur un signal périodique dont le spectre est fourni. Mettre en évidence l'influence des caractéristiques du filtre sur l'opération de filtrage.

ELN A : Stabilité des systèmes linéaires

contenus	capacités exigibles
Fonction de transfert d’un système entrée-sortie linéaire continu et invariant. Stabilité.	Transposer la fonction de transfert opérationnelle dans les domaines fréquentiel (fonction de transfert harmonique) ou temporel (équation différentielle). Étudier la stabilité d’un système d’ordre 1 ou 2 à partir des signes des coefficients de l’équation différentielle ou de la fonction de transfert.

Questions de colles PTSI n°1

Questions (cliquer pour afficher/cacher) Représenter la maille c.f.c.. Déterminer la population et la compacité. Représenter la maille c.f.c.. Localiser les sites tétraédriques, les dénombrer en justifiant et déterminer leur habitabilité. Représenter la maille c.f.c.. Localiser les sites octaédriques, les dénombrer en justifiant et déterminer leur habitabilité. Établir les équations mécanique et électrique des rails de Laplace utilisés comme un moteur, c’est-à-dire fermés sur un générateur extérieur de fém $E_{0}$. On tiendra compte de la résistance $r$ des rails. Établir les équations mécanique et électrique des rails de Laplace utilisés comme un générateur, c’est-à-dire dont la tige mobile est tractée par une force constante ${\overrightarrow {F}}_{0}$. On tiendra compte de la résistance des rails. Procéder au bilan de puissances sur l’un des deux exemples précédents et l’interpréter. Les équations électrique et mécanique seront données par l’interrogateur. Définir le moment magnétique d’une spire plane et rappeler (sans démonstration) l’expression du couple de Laplace qu’elle subit lorsqu’elle est placée dans un champ magnétique uniforme. Un schéma est indispensable pour définir correctement les orientations. Rappeler le modèle du transformateur idéal et établir la loi des tensions.

Réponses (cliquer pour afficher/cacher) Pour la représentation, voir Rappels de cristallographie. Population : $Z=8/8+6/2+1=4$. Compacité : ${\mathcal {C}}=\pi {\sqrt {2}}/6$. Pour la représentation, voir Rappels de cristallographie. Ils sont aux centres des huit huitièmes de cube et donc au nombre de huit et leur habitabilité est $R+R_{T}={\frac {a{\sqrt {3}}}{4}}$. Pour la représentation, voir Rappels de cristallographie. Ils sont aux milieux des douze arêtes et au centre du cube et donc au nombre de quatre (12/4+1) et leur habitabilité est $R+R_{O}={\frac {a}{2}}$. Voir cours de PTSI. Voir cours de PTSI. Pour obtenir un bilan de puissances électriques, on multiplie l'équation électrique par l'intensité du courant. Pour obtenir un bilan de puissances mécaniques, on multiplie l'équation mécanique par la vitesse. Une spire parcourue par une intensité de courant i est orientée selon ce courant par la règle de la main droite, ce qui définit le vecteur normal unitaire ${\vec {n}}$. En notant S l'aire de la surface plane enlacée par le contour, son moment magnétique est défini par ${\vec {m}}=iS{\vec {n}}$. Quand elle est placée dans un champ magnétique uniforme ${\vec {B}}$, elle subit le couple de Laplace ${\vec {\mathcal {\Gamma }}}_{Lapl}={\vec {m}}\wedge {\vec {B}}$. Un transformateur idéal se modélise par deux bobinages autour d’un noyau ferromagnétique parfait dont on admet qu’il canalise parfaitement les lignes de champ magnétique. Par conséquent, le flux $\Phi$ au travers d’une spire du bobinage primaire est égal au flux au travers d’une spire du bobinage secondaire. Le résultat s’obtient en appliquant la loi de Faraday aux deux bobinages en tenant compte du nombre de spires : en régime variable (et au signe près sur les orientations), ${\frac {u_{2}}{N_{2}}}={\frac {u_{1}}{N_{1}}}$.

TIPE (mis à jour le 13 mai 2025)

Généralités

• Introduction au TIPE
• Attendus pédagogiques
• Lien vers la partie « Ingénierie » de la bibliothèque de la Sorbonne
• Site de dépôt de présentation pour vos passages en TIPE pendant l'année

• Calendrier TIPE (cliquer pour afficher)

Calendrier session 2025

Étape 1	Titre et MCOT	du 16 janvier à 9 h	au	6 février 2024 à 14 h
Étape 2	Présentation	du 25 février à 9 h	au	10 juin 2024 à 14 h
Étape 3	Validation	du 12 juin à 9 h	au	19 juin 2024 à 14 h

Mise en forme minimale

• pdf en format 4/3 (largeur/hauteur).
• Diapositive de titre.
• Diapositive d'introduction et objectifs.
• Diapositive de plan (sommaire).
• Diapositives de développements du plan.
• Diapositive de conclusion.

Les diapositives doivent être numérotées.

• Un exemple de présentation LibreOffice à adapter à vos besoins/goûts puis à exporter au format pdf.

Matériels et labo de physique pour le TIPE

Le laboratoire de physique est accessible les lundis de 16 h à 18 h. On prévient le professeur et on remplit le formulaire le plus tôt possible et au plus tard le mercredi avant la date voulue.

• Remplir le formulaire.

Quelques éléments de code utile pour le TIPE

• Code pour tracer un histogramme
• Code pour calculer un écart-type échantillonnal
• Feuille de calcul LibreOffice utilisant DROITEREG
• Code pour réaliser un ajustement affine
• Code pour tracer des barres d'incertitudes
• Code d'une étude complète de la loi de Hooke
• Code pour simuler une variabilité uniforme
• Code pour simuler une variabilité gaussienne
• Code pour simuler une incertitude-type composée
• Aide-mémoire NumPy
• Aide-mémoire Matplotlib

Moteurs de recherche spécialisés

• Archives de la science ouverte
  • en physique
  • en sciences de l'ingénieur
• Google Livres
• Google Publications scientifiques

Documentations, scripts et logiciels

• Un site qui regorge de choses utiles : « Les fiches CPGE », notamment les rubriques :
  • Python
  • Logiciels

Tracking video

• Tracker : analyse de vidéo (pointeur/traqueur) et outils de modélisation associés
  • Tutoriel 1
  • Tutoriel 2
  • Tutoriel 3
• Pymecavideo
  • aide de base
  • Chronophotographie
  • Capture automatique sur vidéo de pendule
  • Vidéo de suivi automatique de points

Plans de cours

Compétences transverses

• Plan CT

Électronique

• Plan ELN-A
• Plan ELN-B
• Plan ELN-C

Optique ondulatoire

• Plan OPT-A
• Plan OPT-B

Thermodynamique

• Plan THE-A
• Plan THE-B
• Plan THE-C
• Plan THE-D
• Plan THE-E
• Plan THE-F

Mécanique des fluides

• Plan MF-A
• Plan MF-B
• Plan MF-C

Électromagnétisme

• Plan ELM-A
• Plan ELM-B
• Plan ELM-C
• Plan ELM-D

Thermodynamique et cinétique électrochimiques

• Plan TCE-A
• Plan TCE-B
• Plan TCE-C
• Plan TCE-D

Documents de cours

Compétences transverses

• Polycopié
• Code pour tracer un histogramme
• Code pour calculer un écart-type échantillonnal
• Feuille de calcul LibreOffice utilisant DROITEREG
• Code pour réaliser un ajustement affine
• Code pour tracer des barres d'incertitudes
• Code d'une étude complète de la loi de Hooke
• Code pour simuler une variabilité uniforme
• Code pour simuler une variabilité gaussienne
• Code pour simuler une incertitude-type composée
• Aide-mémoire NumPy
• Aide-mémoire Matplotlib
• Table de Student

Compléments mathématiques

• Polycopié

Listes de toutes les démonstrations de cours exigibles

• Démonstrations de cours exigibles PT
• Démonstrations de cours exigibles PTSI

Listes des ordres de grandeur exigibles

• Ordres de grandeur exigibles

Travail en autonomie

• Cahier d'entraînement Deuxième année

Rappels de PTSI

• Cahier d'entraînement Première année
• Vocabulaire de la chimie
• Rappels de cristallographie
• Rappels d'induction et sur les forces de Laplace
• Rappels sur les sources lumineuses
• Espèces acido-basiques à connaître
• Comment équilibrer une équation-bilan redox ?
• Oxydants et réducteurs à connaître et demi-équations électroniques
• Rappels de thermodynamique

Électronique

• Diagramme de Bode en gain du passe-bande d'ordre deux
• Diagramme de Bode en gain du passe-haut d'ordre deux
• Diagramme de Bode en gain du passe-bas d'ordre deux
• Script python illustrant l'effet du facteur de qualité sur le diagramme de Bode d'un filtre passe-bande d'ordre deux
• ELN-C : Résumé des critères d'oscillations sinusoïdales

Mécanique des fluides

• Site windfinder de visualisation de carte de courant de vents. Dans « style de carte » : bords = lagrangienne, gradient = eulérienne.
• Vidéo de visualisation de lignes de courant et de types d'écoulement autour d'une aile d'avion.
• MF-A: Baromètre de Torricelli et théorème de Pascal
• MF-C : Vidange d'un réservoir

Thermodynamique

• THE-E : Exemples de diagrammes de fluides réels
• THE-G : Analogies électro-thermiques

Optique ondulatoire

• « Réseau en transmission » sur le site de l'académie de Normandie.
• OPT-B : document support sur les fentes d'Young
• « Fentes d'Young » sur le site de l'Institut d'optique.
• OPT-B  : document support sur le Michelson
• « Michelson » sur le site de l'Institut d'optique.
• « L'interféromètre de Michelson, configuration en lame d'air » sur le site de l'ENS Lyon.

Électromagnétisme

• ELM-A : Analogies électro-gravitationnelles
• ELM-D-IV : Exemples de bilan d’énergie
• Visualisations :
  • Coordonnées cylindriques en 3D
  • Coordonnées sphériques en 3D
  • Ondes progressives
  • Polarisation d'une onde électromagnétique
  • Effet d'un polariseur
  • Réflexion sur un conducteur
• ELM-E-III : Courants surfaciques

Thermodynamique et cinétique électrochimique

• TCE-A : Relation barycentrique
• Document de culture générale sur les accumulateurs lithium-ion

Questions de colles PTSI

Toutes les questions de colles PTSI

Travaux dirigés

Compétences transverses

• PTSI-TD-0

Cristallographie

• PTSI-TD-1

Induction et forces de Laplace

• PTSI-TD-2

Électronique

• ELN-TD-1

Travaux pratiques

• Cahier des charges de l'épreuve de TP Banque PT

Thermodynamique

• PTSI-TP-1 Calorimétrie | Feuille de calcul utilisant DROITEREG (ods) | Feuille de calcul utilisant DROITEREG (xlsx) | Notice multimètre MX 54C
• THE-TP-1 Mesure d'une enthalpie standard

Électronique

• ELN-TP-1 Filtrage analogique
• ELN-TP-2 ALI (1)
• ELN-TP-3 ALI (2)
• ELN-TP-4 Oscillateurs quasi-sinusoïdaux
• ELN-TP-5 Oscillateurs de relaxation
• ELN-TP-6 Électronique numérique

Chimie

• PTSI-TP-2 Dosage acide-base
• PTSI-TP-3 Potentiométrie

Optique

• PTSI-TP-4 Goniomètre
• PTSI-TP-5 Focométrie
• Vidéo du labo de Saint-Louis, présentant l'interféromètre de Michelson
• Vidéo du labo de Saint-Louis, présentant les réglages initiaux de l'interféromètre de Michelson
• OPT-TP-1 Spectroscope
• OPT-TP-2 Michelson (1)
• OPT-TP-3 Trous d'Young
• OPT-TP-4 Michelson (2) (en couleurs)

Électromagnétisme

• ELM-TP-1 Polarisation
• ELM-TP-2 Ondes centimétriques

Mécanique des fluides

• MF-TP-1 Pertes de charge

Capacités numériques

• CN-Activité-PTSI (méthode d'Euler explicite et applications)

Devoirs

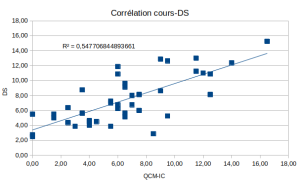
Corrélation entre notes en interro/QCM de cours et notes en DS pour la classe de PT 2024-2025 du lycée Voltaire. Le coefficient de détermination (r² = 0,756) signifie que, si on admet l'hypothèse que les notes en interro/QCM traduisent la connaissance du cours et que cette connaissance est un paramètre d'influence affine sur les notes de DS, alors on peut expliquer 75,6 % des écarts de notes en DS entre deux élèves par leurs écarts de connaissance du cours. Les autres paramètres d'influence pouvant expliquer les 24,4 % restants sont, par exemple : le travail personnel des TD et TP (y compris les corrigés), l'investissement dans les révisions pour les colles, l'appétence pour tel ou tel type d'exercice ou de thématique, la stratégie pendant le DS, la fatigue, la chance, le stress, etc.

• Codes de correction

Textes officiels

• Programme officiel de Physique-chimie en PT
• Programme officiel de Physique-chimie en PTSI
• Rapport de jury des écrits de physique-chimie
• Rapport de jury des oraux de physique-chimie
• Rapport de jury des oraux de manipulation de physique
• Cahier des charges Épreuve A
• Cahier des charges Épreuve B Partie Chimie
• Cahier des charges Épreuve B Partie Thermodynamique (inclut la Mécanique des fluides)
• Cahier des charges de l'épreuve orale de physique-chimie
• Cahier des charges de l'épreuve orale de manipulation de physique

• Programme de physique-chimie de PT détaillé par blocs (cliquer pour afficher)

• 1.1. Éléments de statique des fluides dans un référentiel galiléen
• 1.2. Expression différentielle des principes de la thermodynamique
• 1.3. Diagrammes d'état des fluides réels purs
• 1.4. Description d’un fluide en écoulement stationnaire dans une conduite
• 1.5. Énergétique des fluides en écoulement dans une conduite (a)
• 1.5. Énergétique des fluides en écoulement dans une conduite (b)
• 1.6.1. Étude de quelques dispositifs d’une installation industrielle
• 1.6.2. Cycles industriels
• 2.1. Stabilité des systèmes linéaires
• 2.2. Rétroaction
• 2.3. Oscillateurs
• 2.4. Électronique numérique
• 3.1. Modèle scalaire des ondes lumineuses
• 3.2. Superposition d’ondes lumineuses
• 3.3. Exemple de dispositif interférentiel par division du front d’onde : trous d'Young
• 3.4. Exemple de dispositif interférentiel par division d’amplitude : interféromètre de Michelson
• 4.1. Électrostatique
• 4.2. Magnétostatique
• 4.3. Équations de Maxwell
• 4.4. Énergie du champ électromagnétique
• 4.5. Propagation
• 5.1. Premier principe de la thermodynamique appliqué aux transformations physico-chimiques
• 5.2. Deuxième principe de la thermodynamique appliqué aux transformations physico-chimiques
• 6.1. Étude thermodynamique des réactions d’oxydo-réduction
• 6.2. Étude cinétique des réactions d’oxydo-réduction : courbe courant-potentiel
• 6.3. Stockage et conversion d‘énergie chimique dans des dispositifs électrochimiques
• 6.4. Corrosion humide ou électrochimique

Autres pages web des prépas du lycée Voltaire

• Forum
• Accueil PT
  • Cahier de prépa de la PT
• Accueil PTSI
  • Informations Parcoursup PTSI
  • Cahier de prépa de la PTSI